| .devcontainer | ||
| .github | ||
| cmake | ||
| data | ||
| include | ||
| markdown | ||
| src | ||
| .gitignore | ||
| CMakeLists.txt | ||
| normals.cpp | ||
| obj.cpp | ||
| quad_subdivision.cpp | ||
| README.md | ||
Computer Graphics Lab3 – Meshes
Deadline: Nov. 15 2024, 22:00
Building using CMake
Windows
If your CMake version < 3.16.0, you might see an error pop up while using CMake, saying that Libigl requires a version >= 3.16.0. If you don't want to update your CMake, simply go to the line throwing that error and change the version:
# on my machine the error is thrown in
# "out/build/x64-Debug/_deps/libigl-src/CMakeLists.txt" on line 12:
set(REQUIRED_CMAKE_VERSION "3.16.0")
# change this to a version <= your version, for example:
set(REQUIRED_CMAKE_VERSION "3.0.0")
Linux
If CMake succeeds without errors, great. However, if not, then you will have to resolve the thrown exceptions. We follow libigl's example project in this assignment, which they claim should work on Ubuntu out of the box. It can be however that CMake throws exceptions that look like:
"Could not find X11 (missing: X11_X11_LIB ...)""... headers not found; ... install ... development package""Could NOT find OpenGL (missing: OPENGL_opengl_LIBRARY ...)"
To solve errors like this, install the missing packages (you might need to search around on the web if the following command does not suffice):
sudo apt install libx11-dev libxrandr-dev libxinerama-dev libxcursor-dev libxi-dev libgl1-mesa-dev
WSL (Windows)
Follow the Linux instructions above. Warning: the assignment uses OpenGL and GLFW to create a window, which might not work with WSL. We will not be able to help you here.
MacOS
We follow libigl's example project in this assignment, which they claim should work on MacOS out of the box. If you experience CMake errors that you cannot solve with some help online, please contact us.
Background
Read Section 12.1 of Fundamentals of Computer Graphics (4th Edition).
Skim read Chapter 11 of Fundamentals of Computer Graphics (4th Edition).
There are many ways to store a triangle (or polygonal) mesh on the computer. The data-structures have very different complexities in terms of code, memory, and access performance. At the heart of these structures, is the problem of storing the two types of information defining a mesh: the geometry (where are points on the surface located in space) and the connectivity (which points are connected to each other). The connectivity is also sometimes referred to as the topology of the mesh.
The graphics pipeline works
on a per-triangle and per-vertex basis. So the simplest way to store geometry is
a 3D position for each
-th vertex of the mesh. And to store
triangle connectivity as an ordered triplet of indices referencing vertices:
defines a triangle with corners at vertices
,
and
.
Thus, the geometry is stored as a list of
3D vectors: efficiently, we can
put these vectors in the rows of a real-valued matrix
. Likewise,
the connectivity is stored as a list of
triplets: efficiently, we can put
these triplets in the rows of an integer-valued matrix
.
Question: What if we want to store a (pure-)quad mesh?
Texture Mapping
Texture mapping is a process for mapping image information (e.g., colors) onto a surface (e.g., triangle mesh). The standard way to define a texture mapping is to augment the 3D geometric information of a mesh with additional 2D parametrization information: where do we find each point on the texture image plane? Typically, parameterization coordinates are bound to the unit square.
Mapping a 3D flat polygon to 2D is rather straightforward. The problem of finding a good mapping from a 3D surface to 2D becomes much harder if our surface is not flat (e.g., like a hemisphere), if the surface does not have exact one boundary (e.g., like a sphere) or if the surface has "holes" (e.g., like a torus/doughnut).
Curved surfaces must get distorted when flattened onto the plane. This is why Greenland looks bigger than Africa on a common map of the Earth.
The lack or presence of too many boundaries or the presence of "doughnut holes" in surfaces implies that we need to "cut" the surface to lay out it on the plane so all parts of the surface are "face up". Think about trying to flatten a deflated basketball on the ground.
Normals
For a smooth surface, knowing the surface geometry (i.e., position in space) near a point fully determines the normal vector at that point.
For a discrete mesh, the normal is only well-defined in the middle of planar faces (e.g., inside the triangles of a triangle mesh, but not along the edges or at vertices). Furthermore, if we use these normals for rendering, the surface will have a faceted appearance. This appearance is mathematically correct, but not necessarily desired if we wish to display a smooth looking surface.
Phong realized that linearly interpolating normals stored at the corners of each triangle leads to a smooth appearance.
This raises the question: what normals should we put at vertices or corners of our mesh?
For a faceted surface (e.g., a cube), all corners of a planar face should
share the face's normal
.
For a smooth surface (e.g., a sphere), corners of triangles located at the same vertex should share the same normal vector. This way the rendering is continuous across the vertex. A common way to define per-vertex normals is to take a weighted average of normals from incident faces. Different weighting schemes are possible: uniform average (easy, but sensitive to irregular triangulations), angle-weighted (geometrically well motivated, but not robust near zero-area triangles), area-weighted (geometrically reasonable, well behaved). In this assignment, we'll compute area-weighted per-vertex normals:
where is the set of faces neighboring the
-th vertex.
For surfaces with a mixture of smooth-looking parts and creases, it is useful to define normals independently for each triangle corner (as opposed to each mesh vertex). For each corner, we'll again compute an area-weighted average of normals triangles incident on the shared vertex at this corner, but we'll ignore triangle's whose normal is too different from the corner's face's normal:
where is the minimum dot product between two face normals before we declare
there is a crease between them.
.obj File Format
A common file format to save meshes is the .obj file format, which contains a face-based representation. The connectivity/topological data is stored implicitly by a list of faces made out of vertices. Per vertex, three main types of geometric information can be stored:
- 3D position information of a vertex (denoted as
vin the file, andVin the src code) - 3D normal vector information of a vertex (
vn, orNVin src code) - 2D parameterization information (e.g. texture coordinate) of a vertex (
vt, orUVin the src code)
Take a cube for example. You could construct a mesh with 6 faces, each having 1 normal vector, and 4 vertices per face. You could make it so that each vertex has a 2D texture coordinate.
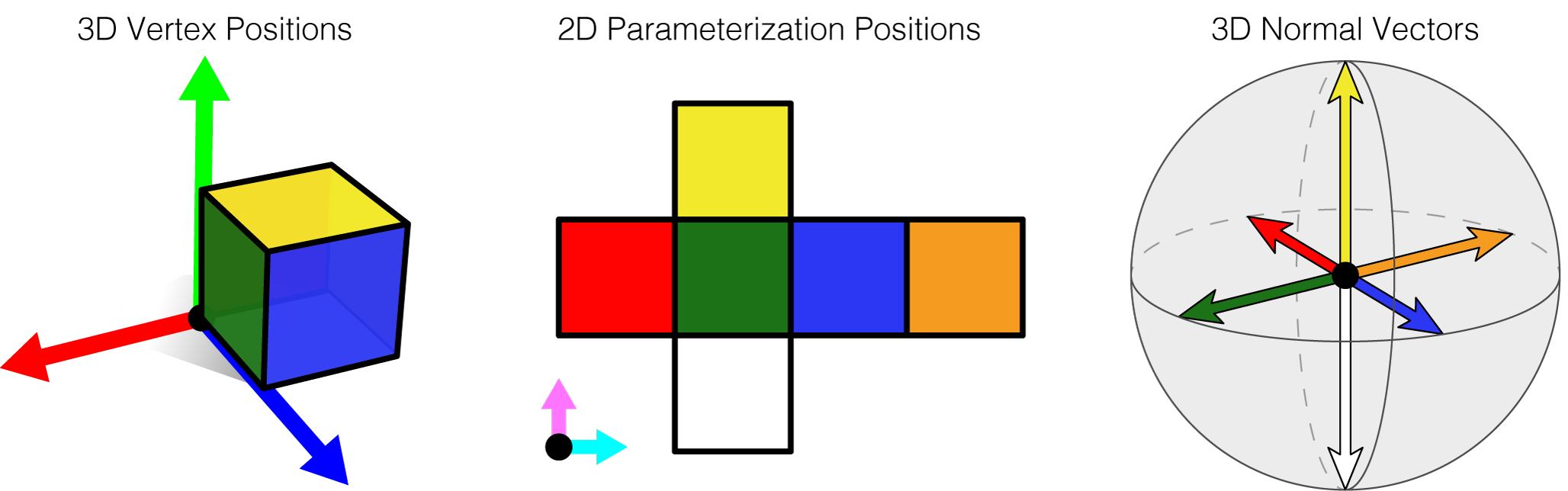
In an .obj file, a face is defined as a list of indices pointing towards certain lines of v, vt and/or vn. For example :
v 0.0 0.0 0.0 # 3D position 1
v 2.0 0.0 0.0 # 2
v 1.0 2.0 0.0 # 3
vt 0.0 0.0 # 2D texture coordinate 1
vt 1.0 0.0 # 2
vt 0.5 1.0 # 3
vn 0.0 0.0 1.0 # 3D normal vector 1
# some examples faces that can be made:
f 1 2 3 # face 1: a face made of 3 vertices, with 3D positions 1,2,3
f 1/1 2/2 3/3 # face 2: same as face 1, but with 2D texture coordinates 1,2,3 respectively
f 1//1 2//1 3//1 # face 3: same as face 1, but with normal vector 1 for each vertex
f 1/1/1 2/2/1 3/3/1 # face 4: each vertex has a position, texture coordinate and normal vector
Warning: In an .obj file, indexing always starts at
1, not0!
This is just an example of course. Faces can have more than 3 vertices, can have vertices with different normal vectors, and the order of faces does not matter.
Subdivision Surfaces
A subdivision surface is a natural generalization of a spline curve. A smooth spline can be defined as the limit of a recursive process applied to a polygon: each edge of the polygon is split with a new vertex and the vertices are smoothed toward eachother. If you've drawn smooth curves using Adobe Illustrator, PowerPoint or Inkscape, then you've used splines.
At a high-level, subdivision surfaces work the same way. We start with a polyhedral mesh and subdivide each face. This adds new vertices on the faces and/or edges of the mesh. Then we smooth vertices toward each other.
The first and still (most) popular subdivision scheme was invented by Catmull (who went on to co-found Pixar) and Clark (founder of Silicon Graphics and Netscape). Catmull-Clark subdivision is defined for inputs meshes with arbitrary polygonal faces (triangles, quads, pentagons, etc.) but always produces a pure-quad mesh as output (i.e., all faces have 4 sides).
To keep things simple, in this assignment we'll assume the input is also a pure-quad mesh.
Mesh Viewers
(Optional) In this assignment, you will create meshes that you can save to an .obj file thanks to write_obj.cpp. If you would like to view these meshes in something other than the libigl viewer we provide, you can open the .obj files in:
-
Mesh Lab free, open-source. Warning: Mesh Lab does not appear to respect user-provided normals in .obj files.
-
Blender: free, open-source. If you want to see the texture, you will have to make a shader with an image texture.
-
Autodesk Maya is a commericial 3D modeling and animation software. They often have free student versions.
Almost ready to start implementing
Eigen Matrices
This assignment use the Eigen library. This section contains some useful syntax:
Eigen::MatrixXi A; // creates a 0x0 matrix of integers
A.resize(10, 3); // resizes the matrix to 10x3 (meaning 10 rows, 3 columns)
Eigen::MatrixXd B; // creates a 0x0 matrix of doubles
B.resize(10, 3); // important, always use resize() !
Eigen::MatrixXd C = Eigen::MatrixXd::Zero(10, 3); // here C.resize() is not necessary
C.row(0) = Eigen::RowVector3d(0, 0, 1); // overwrite the first row of C
C.row(5); // gives the 5th row of C, as an Eigen::RowVectorXd
C(5,0); // gives the element on row=5 and column=0 of C
White list
You're encouraged to use #include <Eigen/Geometry> to compute the cross
product of two 3D vectors
.cross.
Black list
This assignment uses libigl for mesh viewing. libigl has many mesh processing functions implemented in C++, including some of the functions assigned here. Do not copy or look at the following implementations:
igl::per_vertex_normals
igl::per_face_normals
igl::per_corner_normals
igl::double_area
igl::vertex_triangle_adjacency
igl::writeOBJ
Tasks
Part 1: Understanding the .OBJ File Format
Once you have implemented the files below, run
Linux: ./obj ../data/rubiks-cube.png ../data/earth-square.png
Windows: obj.exe ../../../data/rubiks-cube.png ../../../data/earth-square.png
to open a window showing your cube being rendered. If you press 'Escape', it will close and the second window displaying your sphere will pop up. They should look like this:
Tip: look at the header file of each function to implement.
src/write_obj.cpp
The input is a mesh with
- 3D vertex positions (
V) - 2D parametrization positions (
UV) - 3D normal vectors (
NV) - the vertices making up the faces (
F), denoted as indices ofV - the uvs of the faces (
UF), denoted as indices ofUV - the normal vectors of the faces (
UF), denoted as indices ofNV
The goal is to write the mesh to an .obj file.
Note: This assignment covers only a small subset of meshes and mesh-data that the
.objfile format supports.
src/cube.cpp
Construct the quad mesh of a cube including parameterization and per-face normals.
Hint: Draw out on paper and label with indices the 3D cube, the 2D parameterized cube, and the normals.
src/sphere.cpp (optional, not included in rating)
Construct a quad mesh of a sphere with num_faces_u × num_faces_v faces. Take a look at UV spheres or equirectangular projection/mapping.
The equirectangular projection basically defines how a 3D vertex (x,y,z) on the sphere is mapped to a 2D texture coordinate (u,v), and vice versa. To go from (u,v) to (x,y,z) (although some flipping of axes might be necessary):
φ = 2π - 2πu # φ is horizontal and should go from 2π to 0 as u goes from 0 to 1
θ = π - πv # θ is vertical and should go from π to 0 as v goes from 0 to 1
x = sin(θ)cos(φ)
y = cos(θ)
z = sin(θ)sin(φ)
Note
: The
vaxis of the texture coordinate is always upwards
Part 2: Calculating normal vectors
You may assume that the input .obj files will all contain faces with 3 vertices (triangles), like fandisk.obj. Once you have implemented the functions below, run
Linux: ./normals ../data/fandisk.obj
Windows: normals.exe ../../../data/fandisk.obj
to open a window showing the fandisk being rendered using the normals calculated by you. Type '1', '2' or '3' (above qwerty/azerty on the keyboard) to switch between per-face, per-vertex and per-corner normals. The difference between per-face and per-corner is only visible when zoomed in.
Tip: look at the header file of each function to implement.
src/triangle_area_normal.cpp
Compute the normal vector of a 3D triangle given its corner locations. The output vector should have length equal to the area of the triangle.
Important: this the only time where you are allowed to return normal vectors that do not have unit length (i.e. that have not been normalized).
src/per_face_normals.cpp
Compute per-face normals for a triangle mesh. In other words: for each face, compute the normal vector of unit length.
src/per_vertex_normals.cpp
Compute per-vertex normals for a triangle mesh. In other words: for each vertex, compute the normal vector of unit length, by taking a area-weighted average over the normals of all the faces with that vertex as a corner.
src/vertex_triangle_adjacency.cpp
Compute a vertex-triangle adjacency list. For each vertex store a list of all incident faces. Tip: emplace_back().
src/per_corner_normals.cpp
Compute per-corner normals for a triangle mesh. The goal is to compute a unit normal vector for each corner C of each face F. This is done by taking the area-weighted average of normals of faces connected to C. However, an incident face's normals is only included in the area-weighted average if the angle between that face normal and that of F is smaller than a threshold (corner_threshold (= 20 degrees)).
Part 3: Implementing a mesh subdivision method
src/catmull_clark.cpp
Conduct num_iters iterations of Catmull-Clark
subdivision on
a pure quad mesh (V,F).
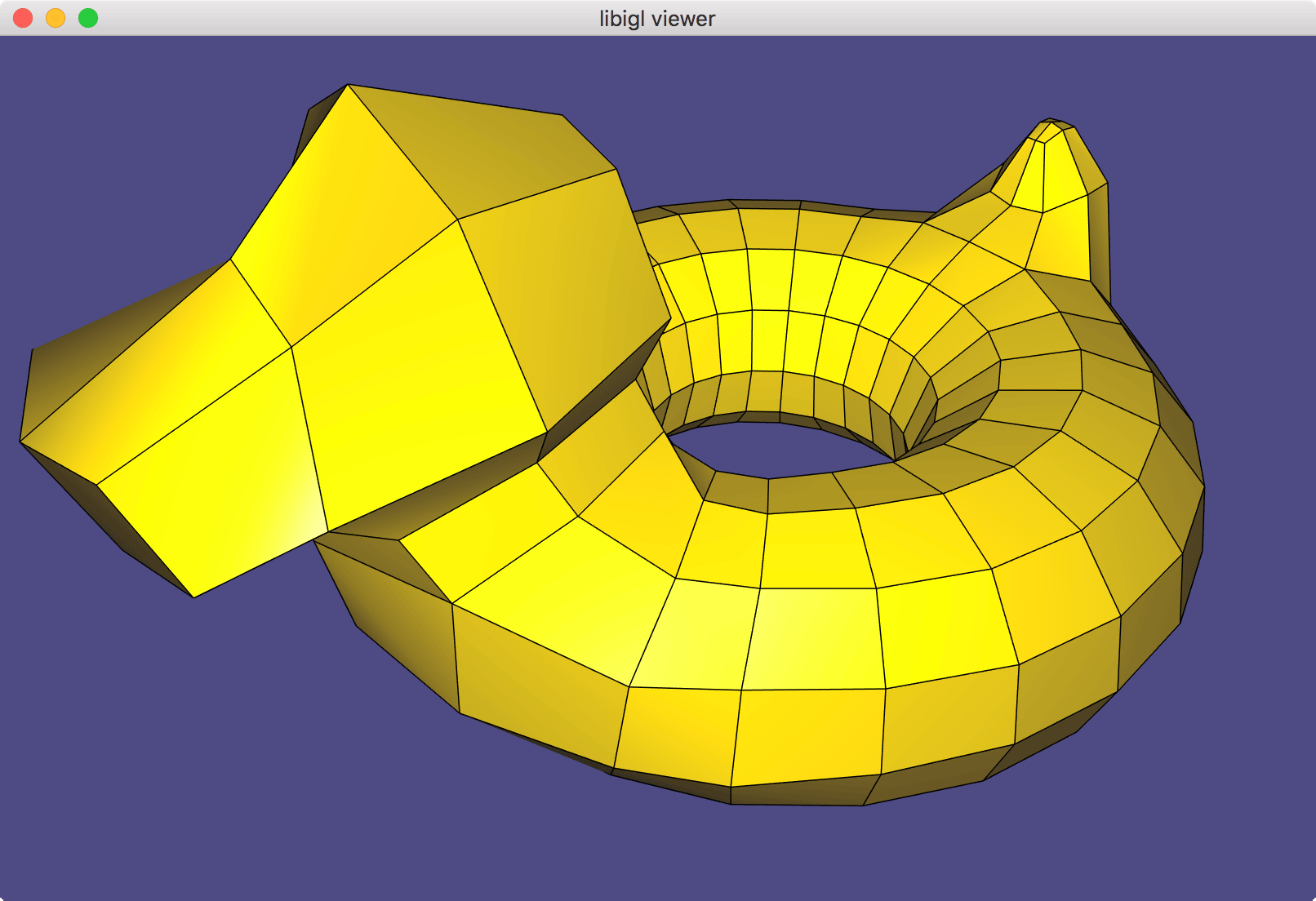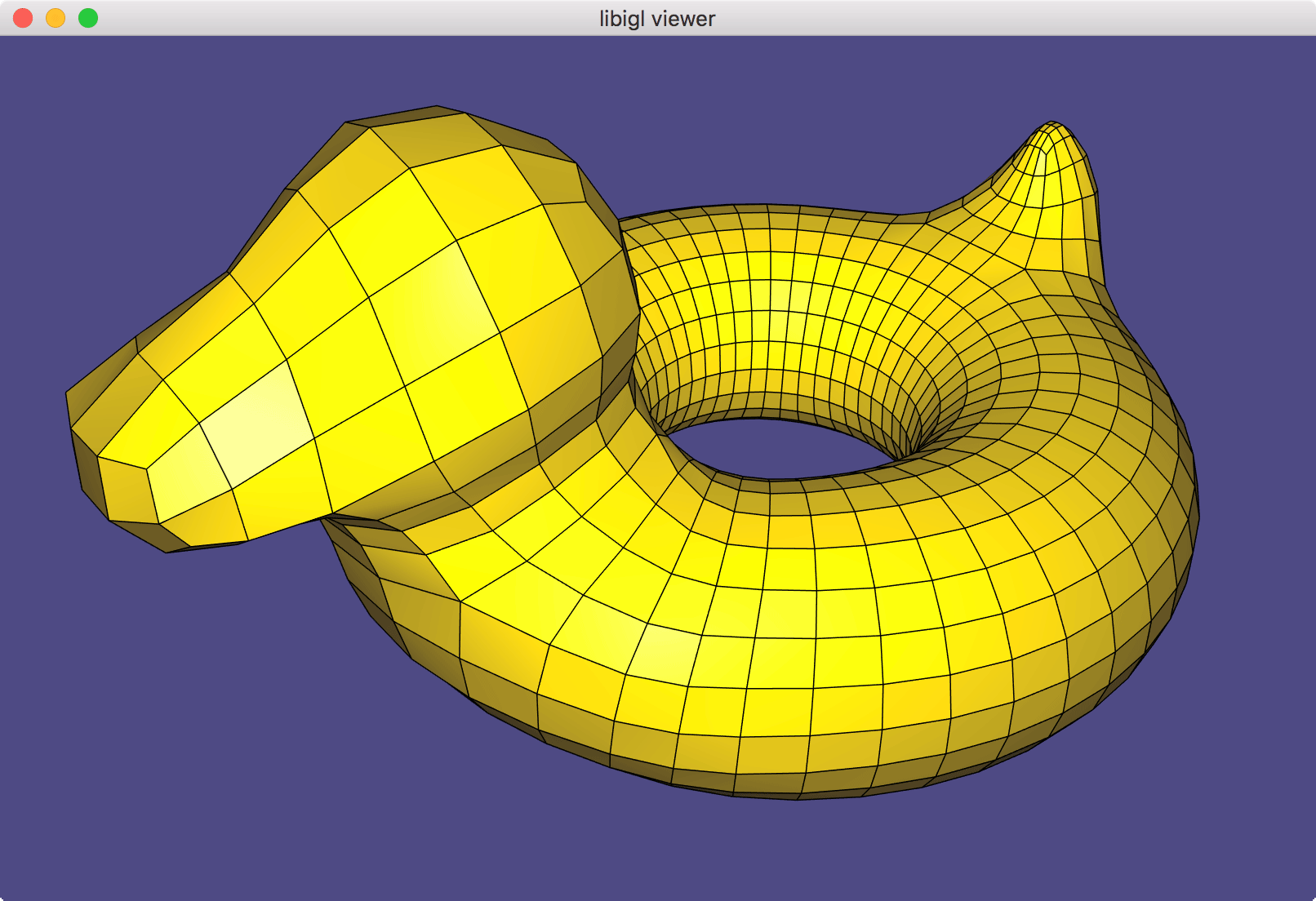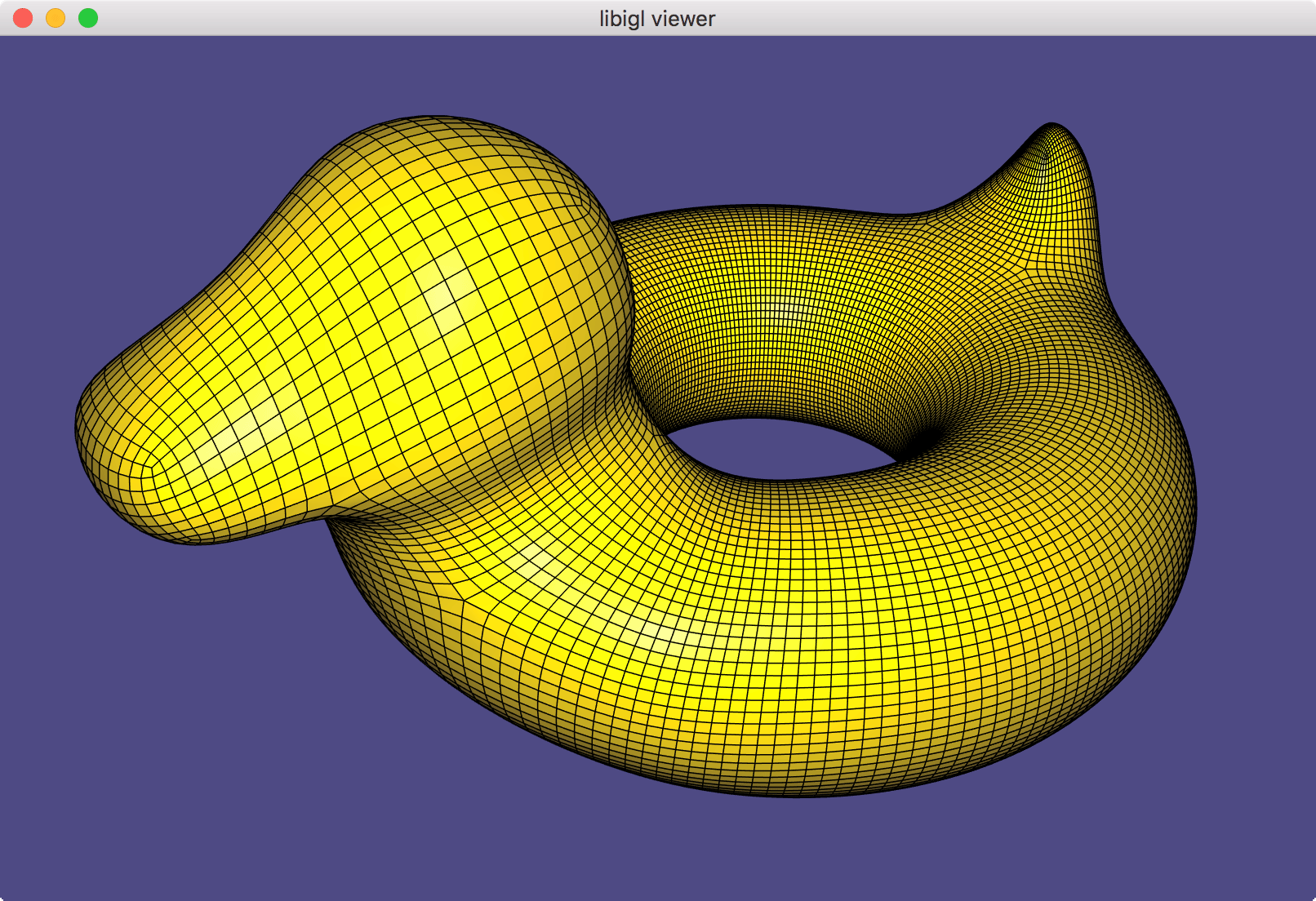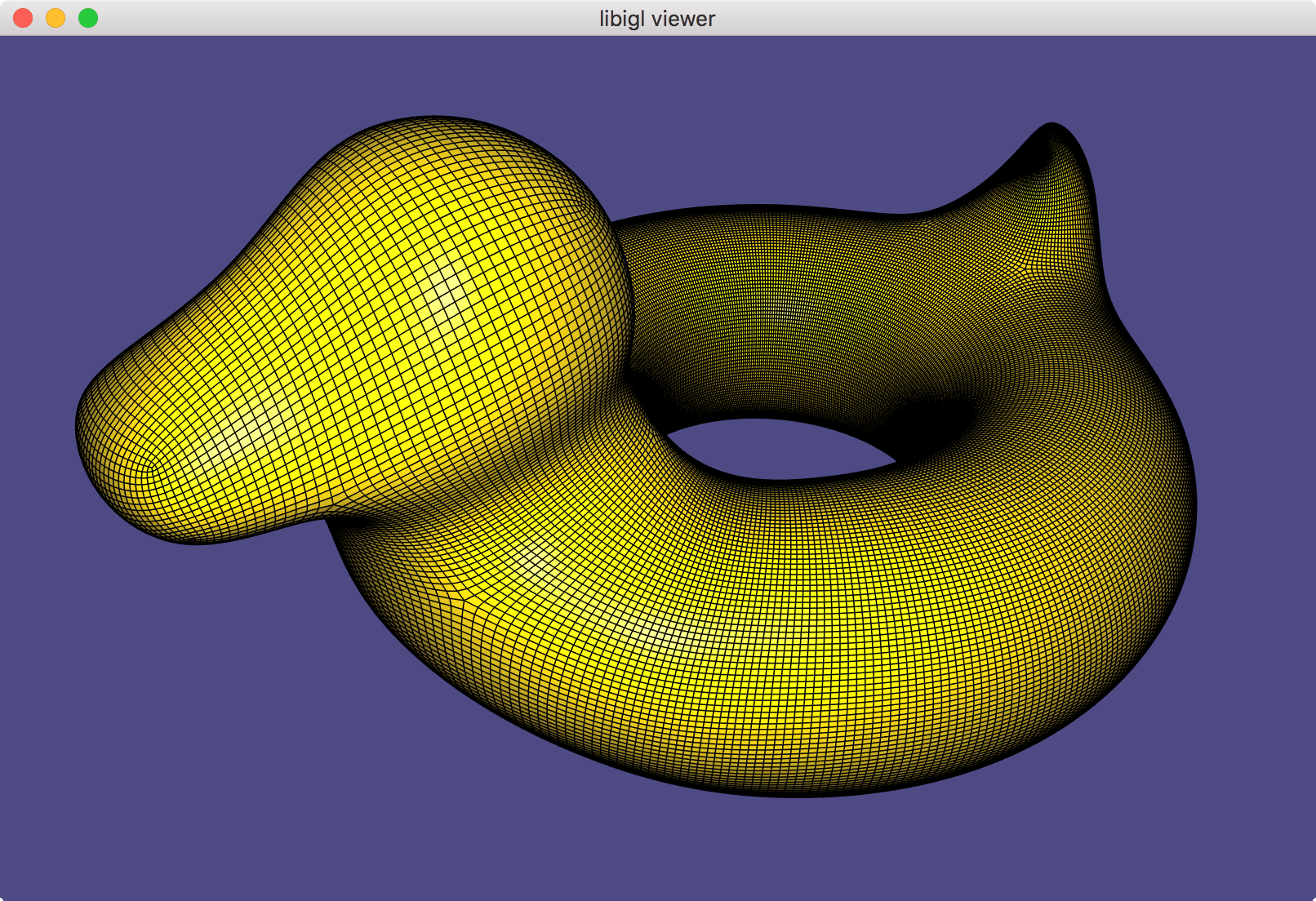
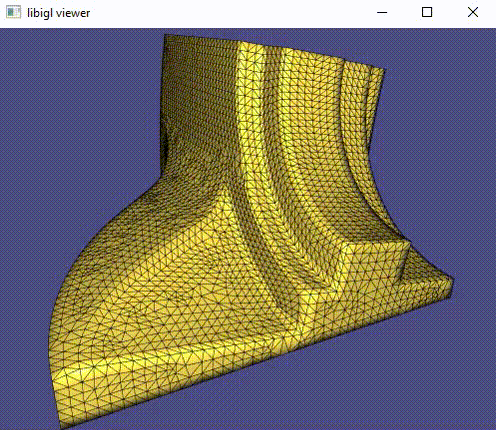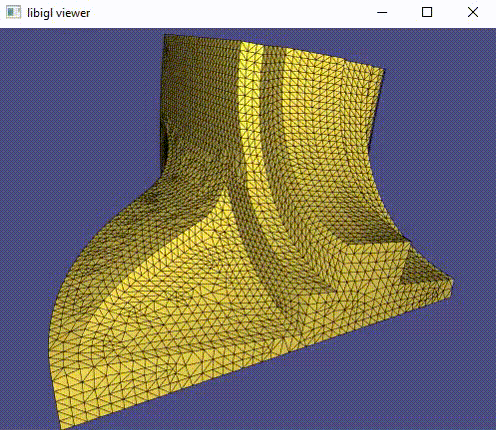
Once this is implemented, run ./quad_subdivision (or quad_subdivision.exe) on your cube.obj or bob.obj (shown earlier). Press 'spacebar' to subdivide once. It should look nicely smooth and uniform from all sides:
Tip: First get cube.obj working before moving onto bob.obj.
Tip: I think the step-by-step explanation on Wikipedia (under "Recursive evaluation") is quite clear.
Tip: perform the Catmull-Clark algorithm on paper first, i.e. draw the cube from cube.obj on a piece of paper and manually calculate each
face point,edge pointandnew vertex point. Check if these values are the same as your implementation.